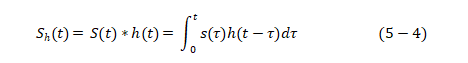您当前的位置： 首页 > 资讯频道 > 新闻资讯 > 应用知识 > 2种技术在超声波信号中高频噪声中的抑制作用（二）

2种技术在超声波信号中高频噪声中的抑制作用（二）

来源： | 发布日期：2022-09-08

前面内容中提到了抑制噪声的一种方法：移动式平均平滑处理。接下来了解下滤波技术。滤波技术是剔除噪声中应用最为广泛的一种方法。通过抑制信号的某些频率成分，滤波可以实现对信号频率的修正。由于任何信号，任意类型（电的，机械的等）的装置都可用频率域的函数来表示，因此，任何装置都可看成是滤波器。

5-5

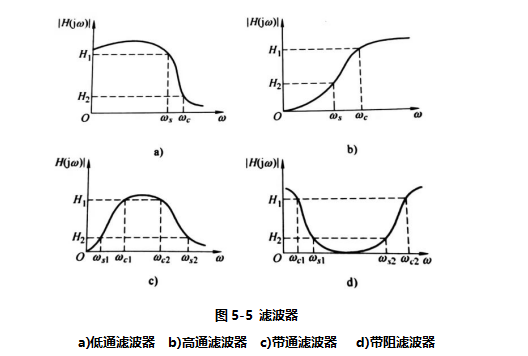
根据滤波器的选频作用，可以把滤波器分成四类，如图5-5所示。其中，ω_c和ω_s分别被称为通带截止频率和阻带截止频率，ω_c 和ω_s之间则称为过滤带。对于低通和高通滤波器，分别各有一个通带、一个阻带和一个过渡带；带通滤波器有两个阻带、一个通带和两个过渡带；而带阻滤波器则有一个阻带、两个通带和两个过渡带。
1)低通滤波器。如图5-5a所示，通带范围是0≦ω ≦ ω_c， ω_c高于为阻带。
2)高通滤波器。通带范围是ω_c≧ ω1，低于ω_c为阻带，如图5-5b所示。
3)带通滤波器。通带范围是ω_c1≦ω≦ ω_c2，通带两侧都为阻带，或是较狭窄的过渡带，如图5-5c所示。
4)带阻滤波器。阻带范围是ω_s1≦ω≦ω_s2，阻带两侧都为通带，或是较狭窄的过渡带，如图5-5d所示。
设某时域信号S(t)，对应的傅里叶变换为s(f)，滤波器传递函数为H(f)。从数学角度看，滤波相当于是s(f)与H(f)的相乘处理[4]，如图5-6所示。

通过频率滤波器后，相当于原时域信号S(t)被修改成为S_h(t)。根据卷积定理，S(t)、S_h(t)以及滤波器对应时域信号h(t)之间存在下列关系:

式中，S(t)为滤波前信号； h(t)为滤波器传递函数H(f)的反博里叶变换。
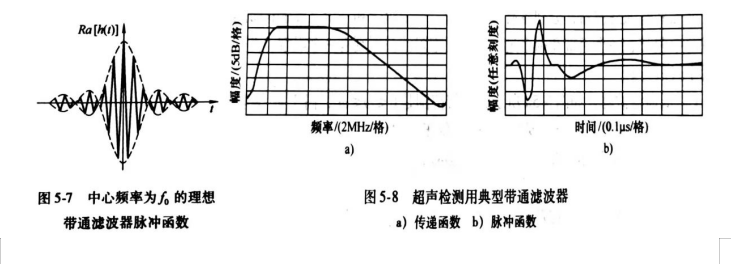
h(t)也称为脉冲函数，因为如果滤波器的输入端为陡直脉冲激励，其具有平坦频谱，则滤波器输出信号正好与此函数相一致。图5-7所示为图5-6中的矩形带通滤波器的脉冲函数。该信号的数学表达式为

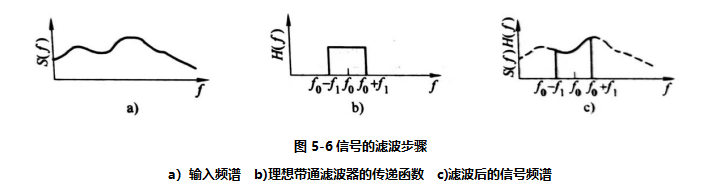
从有理性角度而言，该脉冲函数似乎无物理意义，因为它在时间上存在t<0的情况(意味着输出信号产生在输入激励信号出现之前，有违因果律)。实际的滤波器在通带与阻带之间具有平滑的过渡区，其脉冲函数为一时限函数。图5-8为无损检测中用来优化检测灵敏度的典型带通滤波器。
某些材料中的超声波衰减与频率之间有依从关系，这也可以看做是滤波效应。因此，可以采用材料的传递函数来评价介质的物理和几何特性。

图5.7 5.8