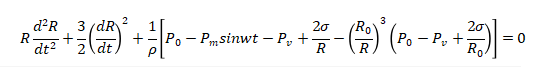热搜关键词： 超声波焊接机生产厂家超声波焊接设备代理批发声峰超声波代理商加盟 ODM代工贴牌 OEM代加工

您当前的位置： 首页 > 资讯频道 > 新闻资讯 > 应用知识 > 超声场中气泡的运动

超声场中气泡的运动

来源： | 发布日期：2022-09-30

为了探讨空化效应的机理，首先必须了解声场中气泡的动态。由于每个空化泡都是独立运动的，因此，研究一个空化泡的发育和闭合过程具有普遍意义。
设液体是不可压缩的，液体中有一气泡，半径为R_o，液体中的静压力为p_o ，声压为 P_msinwt，则由运动方程、连续性方程和空泡表面边界条件，可求得气泡运动遵循的方程式为：

1664519256181

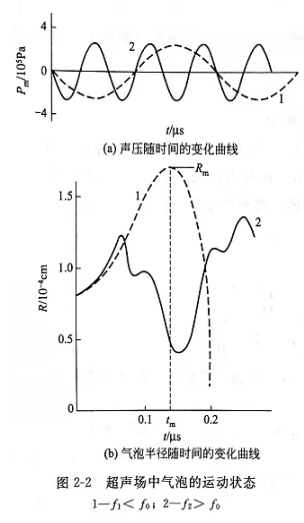
图2-2给出了气泡半径R随时间变化数值解的曲线图形。它是在P₀=P_a， P_m=4×10⁵Pa， R₀=0.8×10^-4cm和频率分别为f₁= 4. 8MHz （对应于曲线1），f₂=14. 3MHz（对应于曲线2）的条件下求解的。图2-2(a)是声压的变化，图2-2(b)是气泡半径随时间的变化。图中曲线1（虚线）对应于声波频率f₁2（是气泡的谐振频率，约为7MHz）的情况。气泡从初始半径R₀= 0.8X10^-4cm在声负压期间不断增长。当声压为正压力时，由于气泡表面振动的惯性作用，仍以某个速度继续膨胀，达到某一最大值后开始收缩，在正压作用下，收缩速度愈来愈大，致使气泡迅速闭合。气泡从最大半径到完全闭合的时间只有秒数量级，它只是声波周期1/4。曲线2（实线）对应于f₂>f₀的情况，气泡表面振动变得很复杂，由图看出气泡是作非线性振动而不会闭合。

1664519274695

由以上所述，可得到这样的结论，即气泡振动和声波频率有关。特别值得注意的是，当气泡半径较大，其谐振频率低于声波频率时，气泡虽可生长发育但却不能闭合。
空化现象中，气泡膨胀到达的最大半径R_m和它膨胀到最大半径的时刻tm是很有意义的。显然，R_m/R₀的数值愈大，则闭合时产生的激波强度愈大。

【本文标签】超声波焊接机超音波塑焊机批发塑料焊接机加工声峰超声波换能器超声波塑焊机厂家

【责任编辑】

上一篇：声峰超声波浅析超声波的反射、透过、折射

下一篇：声峰超声波浅析什么是超声波脉冲反射法

超声波焊接机生产厂家超声波焊接设备代理批发声峰超声波代理商加盟 ODM代工贴牌 OEM代加工

最新资讯

超声波焊接机不发波是怎么回事？2024.04.18

义乌伺服超声波焊接代理加盟—精诚合作2024.04.17

深圳伺服超声波焊接机供应商—诚邀经销商合作加盟2024.04.17

Telsonic超声波发生器常见故障及维修服务2024.04.16
Herrmann海尔曼HiQ系列超声波焊接机故障排除与修复2024.04.15

广州伺服超声波塑焊机源头厂家供应商—加盟合作机会2024.04.12

诚邀杭州伺服超声波焊接机经销商加盟合作2024.04.11

超声波塑焊机在无纺布袋制作中的应用2024.04.11

关于声峰 OEM/ODM/渠道超声波焊接机超声波换能器产品中心加工案例新闻资讯联系我们网站地图

珠海声峰超声波科技有限公司版权所有
备案号：粤ICP备13004144号
邮箱：897808109@qq.com
粤公网安备 44049302000136号

全国服务热线:+86 13612214623
公司总部地址：广东省珠海市香洲区南屏科技工业园屏西五路3号
东莞服务中心：广东省东莞市大朗镇新宝三街48号1栋7楼
汕头服务中心：广东省汕头市澄海区沙港路西片区二横巷7号
宁波服务中心：浙江省宁波市余姚市朗霞街道创业北路南一路1号

添加微信

添加微信

咨询电话

+86 13612214623
微信咨询
返回顶部